
If I focused on a different type, the whole thing will change. Finally, since there are discontinuities within the entire interval, the Electric-Type moves are not continuous on the interval. Some of them show that even one discontinuity can invalidate the entire set, and they can occur at any time of the interval.

So the intervals that are continuous are, ,, ,, , and. – no, 111 and 112 are within the interval.Īnd for a bonus, Mew (#151) is a point of continuity since it’s not a Ground-Type Pokémon (it’s a Psychic-Type Pokémon).– no, 104 and 105 are within the interval.– no, 74, 75, and 76 are within the interval.– no, 31 and 34 are within the interval.

Continuity calculus how to#
Going to the first one, if you’re familiar with how to play Pokémon and how type effectiveness works in normal battle conditions, there are currently only eight type relationships where a move has no effect. Which of the following intervals is the function continuous:, ,, , and. If each interval contains 10 Pokémon, with Bulbasaur being the first Pokémon in the first interval and Mewtwo being the last Pokémon in the last interval, which intervals are globally continuous? A continuity at a point occurs when the move deals any damage, whereas a discontinuity occurs when it has no effect. Suppose an Electric-Type move is used to strike each Pokémon (not including regional forms). The Kanto generation of Pokémon is defined as the first 151 species, where each number represents the National Pokédex number of the species.One is non-mathematical, and the other is mathematical.
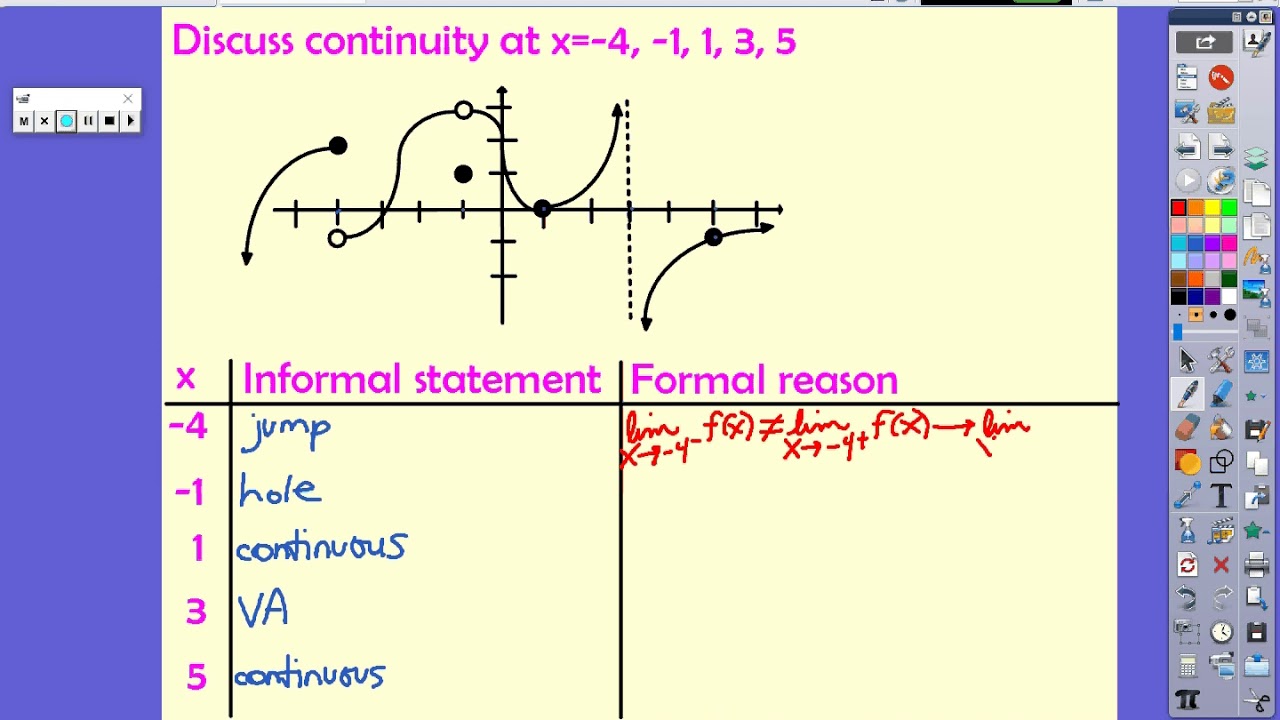
Let’s do two examples of local and global continuity. That’s where the real continuity takes place. The interval is based on the domain, and it can cover as many numbers as it wants. But if there are discontinuities within the interval, then the function is not continuous on the set. If no discontinuities occur within a particular interval, then the function is continuous across the entire set. Global continuity may involve continuity at a point, except that it’s the continuity of a set of point. Does it help the function flow through, or is it considered a disruption? Generally, there’s continuity at a point as long as it’s not on a domain restriction or (in case of piecewise functions) at the end of a function. It’s more about if the point is part of the function. Local continuity is the continuity at a point. Even though it discusses both local continuity and global continuity, the focus is more on global continuity.ĭifference between Local and Global ContinuityĪs a function has both local and global continuity, there is a difference between both types. For a reminder, a function is continuous at a point if it’s defined, the limit exists, and the left-hand limit equals the right-hand limit.

This lesson is on the two types of continuities, based on how many points are continuous. The previous lesson introduced the topic of continuity, which is a property of functions that involves cruising along the graph without disruptions.


 0 kommentar(er)
0 kommentar(er)
